Nonparametric Regression of Stochastic Processes via Signatures
SAM Report, 2023
Alexander Schell, Rima Alaifari
Abstract. Nonparametric regression of stochastic processes estimates statistical relationships between multidimensional, time-dependent data without relying on specific parametric assumptions. We propose a novel approach to this classical estimation problem by using the signature transform from rough path theory to encode the information of a stochastic process into a sequence of iterated integrals, capturing its statistical properties in a time-global and hierarchical manner. Viewing statistical regression as an operator learning problem, this signature-based discretisation allows us to characterise the conditional statistical dependence of a stochastic process on another stochastic process as the solution to a convex semi-infinite linear least squares problem.
This result is based on a functional monotone class argument involving the bounded signature of the conditioning process and allows for the efficient and provably consistent nonparametric estimation of regression functions and conditional distributions for very general classes of jointly distributed stochastic processes as solutions to convex optimisation problems. The structural insights of this approach are summarised in two universally consistent regression estimators that are computable with practical algorithms and supported by broad theoretical guarantees.
On 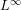 stability for wave propagation and for linear inverse problems
stability for wave propagation and for linear inverse problems
arXiv preprint, 2024
Rima Alaifari, Giovanni S. Alberti, Tandri Gauksson
Abstract. Stability is a key property of both forward models and inverse problems, and depends on the norms considered in the relevant function spaces. For instance, stability estimates for hyperbolic partial differential equations are often based on energy conservation principles, and are therefore expressed in terms of
Multi-Window Approaches for Direct and Stable STFT Phase Retrieval
arXiv preprint, 2024
Rima Alaifari, Yunan Yang
Abstract. Phase retrieval from phaseless short-time Fourier transform (STFT) measurements is known to be inherently unstable when measurements are taken with respect to a single window. While an explicit inversion formula exists, it is useless in practice due to its instability. In this paper, we overcome this lack of stability by presenting two multi-window approaches that rely on a “good coverage” of the time-frequency plane by the ambiguity functions of the windows. The first is to use the fractional Fourier transform of a dilated Gauss function with various angles as window functions. The essential support of a superposition of the ambiguity function from such window functions is of a “daffodil shape”, which converges to a large disc as more angles are used, yielding a much broader coverage in the time-frequency domain. The second approach uses Hermite functions of various degrees as the window functions. The larger the degree, the wider the ambiguity function but with zeros on circles in the time-frequency domain. Combining Hermite functions of different degrees, we can achieve a wide coverage with zeros compensated by the essential support of the ambiguity function from other Hermite windows. Taking advantage of these multi-window procedures, we can stably perform STFT phase retrieval using the direct inversion formula.
Representation Equivalent Neural Operators: a Framework for Alias-free Operator Learning
Conference on Neural Information Processing Systems (NeurIPS) 2023
Francesca Bartolucci, Emmanuel de Bézenac, Bogdan Raonić, Roberto Molinaro, Siddhartha Mishra, Rima Alaifari
Abstract. Recently, there has been significant interest in operator learning, i.e. learning mappings between infinite-dimensional function spaces. This has been particularly relevant in the context of learning partial differential equations from data. However, it has been observed that proposed models may not behave as operators when implemented on a computer, questioning the very essence of what operator learning should be. We contend that in addition to defining the operator at the continuous level, some form of continuous-discrete equivalence is necessary for an architecture to genuinely learn the underlying operator, rather than just discretizations of it. To this end, we propose to employ frames, a concept in applied harmonic analysis and signal processing that gives rise to exact and stable discrete representations of continuous signals. Extending these concepts to operators, we introduce a unifying mathematical framework of Representation equivalent Neural Operator (ReNO) to ensure operations at the continuous and discrete level are equivalent. Lack of this equivalence is quantified in terms of aliasing errors. We analyze various existing operator learning architectures to determine whether they fall within this framework, and highlight implications when they fail to do so.
Convolutional Neural Operators for robust and accurate learning of PDEs
Conference on Neural Information Processing Systems (NeurIPS) 2023
Bogdan Raonić, Roberto Molinaro, Tim De Ryck, Tobias Rohner, Francesca Bartolucci, Rima Alaifari, Siddhartha Mishra, Emmanuel de Bézenac
Abstract. Although very successfully used in conventional machine learning, convolution based neural network architectures — believed to be inconsistent in function space — have been largely ignored in the context of learning solution operators of PDEs. Here, we present novel adaptations for convolutional neural networks to demonstrate that they are indeed able to process functions as inputs and outputs. The resulting architecture, termed as convolutional neural operators (CNOs), is designed specifically to preserve its underlying continuous nature, even when implemented in a discretized form on a computer. We prove a universality theorem to show that CNOs can approximate operators arising in PDEs to desired accuracy. CNOs are tested on a novel suite of benchmarks, encompassing a diverse set of PDEs with possibly multi-scale solutions and are observed to significantly outperform baselines, paving the way for an alternative framework for robust and accurate operator learning.
Towards clinical-dose grating interferometry breast CT with fused intensity-based iterative reconstruction
Opt. Express 31(5), 9052-9071 (2023)
Stefano van Gogh, Michał Rawlik, Alexandre Pereira, Simon Spindler, Subhadip Mukherjee, Marie-Christine Zdora, Martin Stauber, Rima Alaifari, Zsuzsanna Varga, Marco Stampanoni
Abstract. X-ray grating interferometry CT (GI-CT) is an emerging imaging modality which provides three complementary contrasts that could increase the diagnostic content of clinical breast CT: absorption, phase, and dark-field. Yet, reconstructing the three image channels under clinically compatible conditions is challenging because of severe ill-conditioning of the tomographic reconstruction problem. In this work we propose to solve this problem with a novel reconstruction algorithm that assumes a fixed relation between the absorption and the phase-contrast channel to reconstruct a single image by automatically fusing the absorption and phase channels. The results on both simulations and real data show that, enabled by the proposed algorithm, GI-CT outperforms conventional CT at a clinical dose.
Unique wavelet sign retrieval from samples without bandlimiting
arXiv preprint (to appear in Proceedings of the AMS), 2023
Rima Alaifari, Francesca Bartolucci, Matthias Wellershoff
Abstract. We study the problem of recovering a signal from magnitudes of its wavelet frame coefficients when the analyzing wavelet is real-valued. We show that every real-valued signal can be uniquely recovered, up to global sign, from its multi-wavelet frame coefficients
![]()
for every
Iterative phase contrast CT reconstruction with novel tomographic operator and data-driven prior
PLOS ONE, 2022
Stefano van Gogh, Subhadip Mukherjee, Jinqiu Xu, Zhentian Wang, Michał Rawlik, Zsuzsanna Varga, Rima Alaifari, Carola-Bibiane Schönlieb, Marco Stampanoni
Abstract. Breast cancer remains the most prevalent malignancy in women in many countries around the world, thus calling for better imaging technologies to improve screening and diagnosis. Grating interferometry (GI)-based phase contrast X-ray CT is a promising technique which could make the transition to clinical practice and improve breast cancer diagnosis by combining the high three-dimensional resolution of conventional CT with higher soft-tissue contrast. Unfortunately though, obtaining high-quality images is challenging. Grating fabrication defects and photon starvation lead to high noise amplitudes in the measured data. Moreover, the highly ill-conditioned differential nature of the GI-CT forward operator renders the inversion from corrupted data even more cumbersome. In this paper, we propose a novel regularized iterative reconstruction algorithm with an improved tomographic operator and a powerful data-driven regularizer to tackle this challenging inverse problem. Our algorithm combines the L-BFGS optimization scheme with a data-driven prior parameterized by a deep neural network. Importantly, we propose a novel regularization strategy to ensure that the trained network is non-expansive, which is critical for the convergence and stability analysis we provide. We empirically show that the proposed method achieves high quality images, both on simulated data as well as on real measurements.
Localized adversarial artifacts for compressed sensing MRI
SIAM J. Imaging Sci. 16 (4), SC14-SC26, 2023
Rima Alaifari, Giovanni S. Alberti, Tandri Gauksson
Abstract. As interest in deep neural networks (DNNs) for image reconstruction tasks grows, their reliability has been called into question (Antun et al., 2020; Gottschling et al., 2020). However, recent work has shown that compared to total variation (TV) minimization, they show similar robustness to adversarial noise in terms of
On the connection between uniqueness from samples and stability in Gabor phase retrieval
Sampling Theory, Signal Processing, and Data Analysis (to appear), 2023
Rima Alaifari, Francesca Bartolucci, Stefan Steinerberger, Matthias Wellershoff
Abstract. For every lattice
Ill-Posed Problems: From Linear to Nonlinear and Beyond
Harmonic and Applied Analysis. Birkhäuser, Cham, 101-148, 2021
Rima Alaifari
Abstract. Inverse (ill-posed) problems appear in many applications such as medical imaging, astronomy, seismic imaging, nondestructive testing, signal processing, etc. Typically, these problems cannot be solved by conventional methods as they suffer from instabilities and regularization is required. This chapter has evolved from a mini-course taught at the Summer School on Applied Harmonic Analysis and Machine Learning at the University of Genoa in 2019. It offers an overview of the theory of inverse problems and discusses three ill-posed problems that have been studied rather recently in the literature: limited data reconstruction in computerized tomography, phase retrieval, and image classification with DNNs. The selection highlights that for modern problems, the usefulness of standard theory of regularization can be limited.
Phase retrieval from sampled Gabor transform magnitudes: Counterexamples
Journal of Fourier Analysis and Applications 28 (1), 1-8, 2021
Rima Alaifari, Matthias Wellershoff
Abstract. We consider the recovery of square-integrable signals from discrete, equidistant samples of their Gabor transform magnitude and show that, in general, signals can not be recovered from such samples. In particular, we show that for any lattice, one can construct functions in
Phase retrieval of bandlimited functions for the wavelet transform
Applied and Computational Harmonic Analysis, 2023
Rima Alaifari, Francesca Bartolucci, Matthias Wellershoff
Abstract. We study the problem of phase retrieval in which one aims to recover a function
Uniqueness of STFT phase retrieval for bandlimited functions
Applied and Computational Harmonic Analysis 50, 34-48, 2021
Rima Alaifari, Matthias Wellershoff
Abstract. We consider the problem of phase retrieval from magnitudes of short-time Fourier transform (STFT) measurements. It is well-known that signals are uniquely determined (up to global phase) by their STFT magnitude when the underlying window has an ambiguity function that is nowhere vanishing. It is less clear, however, what can be said in terms of unique phase-retrievability when the ambiguity function of the underlying window vanishes on some of the time-frequency plane. In this short note, we demonstrate that by considering signals in Paley-Wiener spaces, it is possible to prove new uniqueness results for STFT phase retrieval. Among those, we establish a first uniqueness theorem for STFT phase retrieval from magnitude-only samples in a real-valued setting.
On Matrix Rearrangement Inequalities
Proceedings of the AMS, Vol. 148, Iss. 5, 2020
Rima Alaifari, Xiuyuan Cheng, Lillian B. Pierce, Stefan Steinerberger
Abstract. Given two symmetric and positive semidefinite square matrices
![]()
Drury [10] has characterized precisely which disordered words have the property that an inequality of this type holds for all matrices
In contrast, we prove that for
Stability estimates for phase retrieval from discrete Gabor measurements
Journal of Fourier Analysis and Applications 27 (2), 1-31, 2021
Rima Alaifari, Matthias Wellershoff
Abstract. Phase retrieval refers to the problem of recovering some signal (which is often modelled as an element of a Hilbert space) from phaseless measurements. It has been shown that, in the deterministic setting, phase retrieval from frame coefficients is always unstable in infinite dimensional Hilbert spaces [5] and possibly severely ill-conditioned in finite dimensional Hilbert spaces [5].
Recently, it was also shown that phase retrieval from measurements induced by the Gabor transform with Gaussian window function is stable when one is willing to accept a more relaxed semi-global stability regime [1].
We present first evidence that this semi-global stability regime allows one to do phase retrieval from measurements induced by the discrete Gabor transform in such a way that the corresponding stability constant only scales linearly in the space dimension. To this end, we utilise well-known reconstruction formulae which have been used repeatedly in recent years [4], [6-8].
Gabor phase retrieval is severely ill-posed
Applied and Computational Harmonic Analysis 50, 401-419, 2021
Rima Alaifari, Philipp Grohs
Abstract. The problem of reconstructing a function from the magnitudes of its frame coefficients has recently been shown to be never uniformly stable in infinite-dimensional spaces [5]. This result also holds for frames that are possibly continuous [2]. On the other hand, the problem is always stable in finite-dimensional settings. A prominent example of such a phase retrieval problem is the recovery of a signal from the modulus of its Gabor transform. In this paper, we study Gabor phase retrieval and ask how the stability degrades on a natural family of finite-dimensional subspaces of the signal domain
ADef: an Iterative Algorithm to Construct Adversarial Deformations
International Conference on Learning Representations (ICLR) 2019
Rima Alaifari, Giovanni S. Alberti, Tandri Gauksson
Abstract. While deep neural networks have proven to be a powerful tool for many recognition and classification tasks, their stability properties are still not well understood. In the past, image classifiers have been shown to be vulnerable to so-called adversarial attacks, which are created by additively perturbing the correctly classified image.
In this paper, we propose the ADef algorithm to construct a different kind of adversarial attack created by iteratively applying small deformations to the image, found through a gradient descent step. We demonstrate our results on MNIST with a convolutional neural network and on ImageNet with Inception-v3 and ResNet-101.
Stable phase retrieval in infinite dimensions
Foundations of Computational Mathematics, Vol. 19, Issue 4, 2019
Rima Alaifari, Ingrid Daubechies, Philipp Grohs, Rujie Yin
Abstract. The problem of phase retrieval is to determine a signal
Recent work [9,3] has shown that, whenever ![]() is infinite-dimensional, phase retrieval is never uniformly stable, and that, although it is always stable in the finite dimensional setting, the stability deteriorates severely in the dimension of the problem [9]. Any finite dimensional approximation of an infinite dimensional problem has to take into account this phenomenon which makes one wonder whether phase retrieval is even advisable in these situations.
is infinite-dimensional, phase retrieval is never uniformly stable, and that, although it is always stable in the finite dimensional setting, the stability deteriorates severely in the dimension of the problem [9]. Any finite dimensional approximation of an infinite dimensional problem has to take into account this phenomenon which makes one wonder whether phase retrieval is even advisable in these situations.
On the other hand, all observed instabilities are of a certain type: they occur whenever the function ![]() of intensity measurements is concentrated on disjoint sets
of intensity measurements is concentrated on disjoint sets ![]() , i.e., when
, i.e., when ![]() where
where ![]() is concentrated on
is concentrated on ![]() (and
(and ![]() ). Indeed, it is easy to see that intensity measurements of any function
). Indeed, it is easy to see that intensity measurements of any function ![]() will be close to those of
will be close to those of ![]() while the functions themselves need not be close at all.
while the functions themselves need not be close at all.
Motivated by these considerations we propose a new paradigm for stable phase retrieval by considering the problem of reconstructing ![]() up to a phase factor that is not global, but that can be different for each of the subsets
up to a phase factor that is not global, but that can be different for each of the subsets ![]() , i.e., recovering
, i.e., recovering ![]() up to the equivalence
up to the equivalence
![]()
We present concrete applications (for example in X-ray diffraction imaging or audio processing) where this new notion of stability is natural and meaningful and show that in this setting stable phase retrieval can actually be achieved, for instance if the measurement system is a Gabor frame or a frame of Cauchy wavelets.
Phase retrieval in the general setting of continuous frames for Banach spaces
SIAM Math Analysis Vol. 49 Issue 3, 2017
Rima Alaifari, Philipp Grohs
Abstract. We develop a novel and unifying setting for phase retrieval problems that works in Banach spaces and for continuous frames and consider the questions of uniqueness and stability of the reconstruction from phaseless measurements. Our main result states that also in this framework, the problem of phase retrieval is never uniformly stable in infinite dimensions. On the other hand, we show weak stability of the problem. This complements recent work [9], where it has been shown that phase retrieval is always unstable for the setting of discrete frames in Hilbert spaces. In particular, our result implies that the stability properties cannot be improved by oversampling the underlying discrete frame.
We generalize the notion of complement property (CP) to the setting of continuous frames for Banach spaces (over ![]() or
or ![]() ) and verify that it is a necessary condition for uniqueness of the phase retrieval problem; when
) and verify that it is a necessary condition for uniqueness of the phase retrieval problem; when ![]() the CP is also sufficient for uniqueness. In our general setting, we also prove a conjecture posed by Bandeira et al. [5], which was originally formulated for finite-dimensional spaces: for the case
the CP is also sufficient for uniqueness. In our general setting, we also prove a conjecture posed by Bandeira et al. [5], which was originally formulated for finite-dimensional spaces: for the case ![]() the strong complement property (SCP) is a necessary condition for stability. To prove our main result, we show that the SCP can never hold for frames of infinite-dimensional Banach spaces.
the strong complement property (SCP) is a necessary condition for stability. To prove our main result, we show that the SCP can never hold for frames of infinite-dimensional Banach spaces.
Reconstructing real-valued functions from unsigned coefficients with respect to wavelet and other frames
Journal of Fourier Analysis and Applications Vol. 23 Issue 6, 2017
Rima Alaifari, Ingrid Daubechies, Philipp Grohs, Gaurav Thakur
Abstract. In this paper we consider the following problem of phase retrieval: Given a collection of real-valued band-limited functions
We find that under some mild assumptions on the semi-discrete frame and if
We further establish a local stability property of our reconstruction problem. Finally, for two concrete examples of a (discrete) frame of
Stability estimates for the regularized inversion of the truncated Hilbert transform
Inverse Problems Vol. 32, 2016
Rima Alaifari, Michel Defrise, Alexander Katsevich
Abstract. In limited data computerized tomography, the 2D or 3D problem can be reduced to a family of 1D problems using the differentiated backprojection (DBP) method. Each 1D problem consists of recovering a compactly supported function
Lower bounds for the truncated Hilbert transform
Revista Matemática Iberoamericana Vol. 32 Issue 1, 2016
Rima Alaifari, Lillian B. Pierce, Stefan Steinerberger
Abstract. Given two intervals
![]()
for some constants
Asymptotic analysis of the SVD of the truncated Hilbert transform with overlap
SIAM Math Analysis Vol. 47 Issue 1, 2015
Rima Alaifari, Michel Defrise, Alexander Katsevich
Abstract. The truncated Hilbert transform with overlap
the singular values approach zero and one. In this paper, we exploit the property that
Spectral analysis of the truncated Hilbert transform with overlap
SIAM Math Analysis Vol. 46 Issue 1, 2014
Reema Al-Aifari, Alexander Katsevich
Abstract. We study a restriction of the Hilbert transform as an operator
The continuous Procrustes distance between two surfaces
Communications on Pure and Applied Mathematics Vol. 66 Issue 6, 2013
Yaron Lipman, Reema Al-Aifari, Ingrid Daubechies
Princeton University
Abstract. The Procrustes distance is used to quantify the similarity or dissimilarity of (3-dimensional) shapes, and extensively used in biological morphometrics. Typically each (normalized) shape is represented by

Comments are closed.